最短路径算法
整理于网络
- 单源最短路
不带负权边:Dijkstra
带负权边:Bellman−Ford、SPFA - 多源最短路:
Floyd
Dijkstra
假设图中顶点V个,边E条,有如下结论
- 这是求解单元最短路径的经典算法,非常重要
- 其本质是贪心+
BFS Dijkstra算法更适合稠密图(边多的)- 无论图有没有环,
Dijkstra算法都是可以用的,它只是不能处理负权边,因为它本质上是贪心策略,每个点选择之后就不再更新,如果碰到了负边的存在就会破坏这个贪心的策略就无法处理了。 - 堆优化+邻接矩阵是常用的解法
例题
有 N 个网络节点,标记为 1 到 N。
给定一个列表 times,表示信号经过有向边的传递时间。 times[i] = (u, v, w),其中 u 是源节点,v 是目标节点, w 是一个信号从源节点传递到目标节点的时间。
现在,我们从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1。
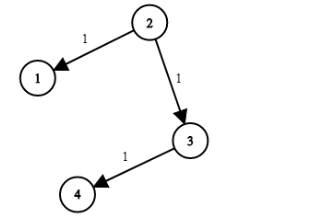
1 | 输入:times = [[2,1,1],[2,3,1],[3,4,1]], N = 4, K = 2 |
堆优化的Dijkstra算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52import javafx.util.Pair;
import java.util.*;
/**
* leetcode-743 网络延迟时间
*
* @author Hongliang Zhu
* @create 2020-07-26 11:03
*/
public class NetworkDelayTime {
public int networkDelayTime(int[][] times, int N, int K) {
int res = 0;
// 建图 , 每个times就是一条边, 每条边包括起始点和终点已经这条边对应的权重
Map<Integer, List<int[]>> Graph = new HashMap<>();
for (int[] time : times) {
Graph.computeIfAbsent(time[0], k -> new ArrayList<>()).add(new int[]{time[1], time[2]});
}
Set<Integer> visited = new HashSet<>();
// 优先级队列,小根堆
PriorityQueue<Pair<Integer, Integer>> q = new PriorityQueue<>(Comparator.comparingInt(Pair::getValue));
// 将源点加入
q.offer(new Pair<>(K, 0));
while (!q.isEmpty()) {
Pair<Integer, Integer> cur = q.poll();
if (visited.contains(cur.getKey())) {
// 已经访问过了
continue;
}
visited.add(cur.getKey());
res = Math.max(res, cur.getValue());
// 将其相邻的边遍历
for (int[] next : Graph.getOrDefault(cur.getKey(), new ArrayList<>())) {
if (visited.contains(next[0])) {
continue;
}
q.offer(new Pair<>(next[0], next[1] + cur.getValue()));
}
}
return visited.size() == N ? res : -1;
}
public static void main(String[] args) {
NetworkDelayTime solution = new NetworkDelayTime();
int[][] times = {{2, 1, 1}, {2, 3, 1}, {3, 4, 1}};
int result = solution.networkDelayTime(times, 4, 2);
System.out.println(result);
}
}
Bellman-Ford
什么是BF算法

BF这个算法也是求单源最短路径的一个算法,算法非常简洁。但是他并不是一个最优的一个方法,他的时间复杂度大于迪杰斯特拉算法。事实上,BF算法的时间复杂度正比于结点的个数和边个数的乘积,即O(V*E)。而迪杰斯特拉算法可以使用一个小根堆来实现,复杂度更小,是O(E+V)log(V)。
我们使用BF算法,是因为有时候迪杰斯特拉他算法在某些情况下不适用,也就是说图中会有负边权。当图中存在着负边时候,就有可能导致negative cycle。这种情况下,我们需要把它检测出来。如果使用迪杰斯特拉算法的话,会陷入一个循环之中,因为算法总能找到一个更短的路径。
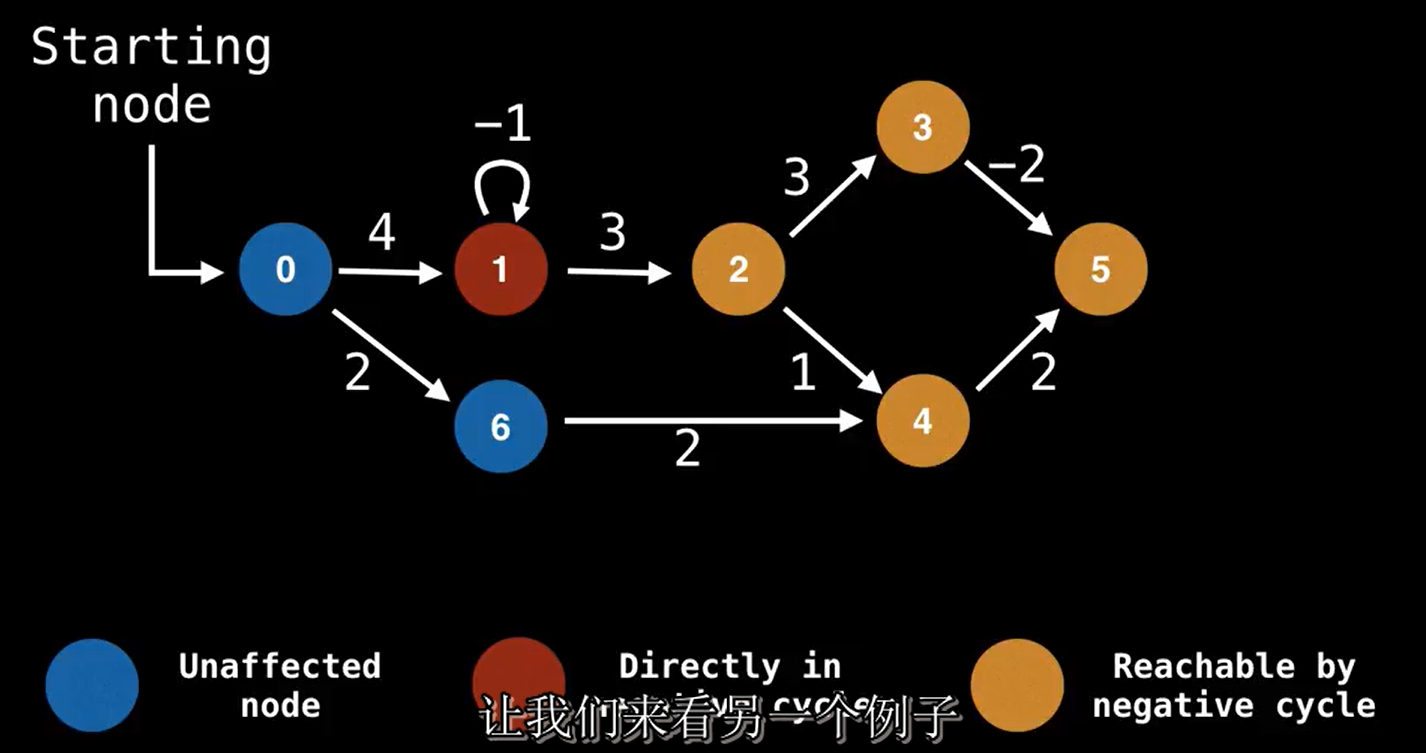
红色的节点表示负环, 经过负环的节点的权重都会是负无穷, 黄色的节点。
BF算法的步骤
E: 边数
V:顶点数
S:开始节点
D:开始节点到其他节点的单源最短路径,是一个大小为V的数组
- 将每个每个节点到开始节点的最短路径设为﹢无穷
- set D[S] = 0, 开始节点到自己为0;
- 对每一条边进行
V-1次松弛操作
松弛操作:
- 对于任意一条边 (u -> v),取出他们存储好的权重 w( u -> v ).
- 如果
u.distance + w < v.distance,那么做两个赋值操作:v.distance = u.distance + w,v.previous = u;这一步是松弛操作的核心。 - 如果上面的判断不成立,什么都不做
问题来了,为啥是V-1次循环呢?
做 n - 1 次已经足够了。算法导论上有证明:
- 从原点开始走,到第 x 个节点,这中间只有 x - 1 条边(不考虑环路)
- 如果一个图有 n 个节点,那么即使用最啰嗦的走法,到达一个点顶多需要走 n - 1 条边(不考虑环路)。也就是顶多把所有的节点都经过一遍。
- 在第一轮对所有的边进行松弛的时候,被松弛的点其实只有从原点可以一步到达的点。其他的点所在的边 Edge( u -> v ) 中,u.distance 都是 ∞,v 无法被松弛。只有 start_point.distance 为 0,Edge( start_point -> v ) 中的 v 才可能被松弛。
- 以此类推,在第 i 轮中,被松弛的点只可能是距离原点 i 步的点。他们利用到的边是 Edge( vi - 1 -> vi),其中 vi - 1 在上一轮松弛的过程中已经被松弛过,如果他能到达原点的话,vi - 1.distance 就不会是 ∞。
- 有些点可能有多种不同的到达方式,并且在第 i 步之前也松弛过。这其实没关系。如果第 i 步是最后一次到达他,所有能用来到达这个点的边都已经被计算机探索过(不然这就不是最后一次到达),所以这次松弛也将是它最后一次被松弛,之后到达他的 distance 就已经是最终结果值了。
- 根据上面提到的 2,不可能有节点出现 n - 1 步还到达不了的地方,即使一个点有多条路径可以到达(除非这个点真的无法到达),他的最多步数路径上的边也都被计算机探索过了。也就是说,他的最后一次被访问已经发生过,他的 distance 肯定已经是最终结果值了。没有任何一个点可以例外。
所以 n - 1 次循环已经足够。
第一次迭代在对所有的边进行松弛之后,得到的是从起点”只能经过一条边“到达其余各顶点的最短路径长度…第k轮迭代得到的就是起始点”最多经过k条边“到达其他各顶点的最短路径长度。
迭代的时候使用边进行松弛的顺序比较随机。在最差情况下,导致第一次迭代后,只更新了从起点出发通过一条边到达的部分顶点的最短路径长度。而没有更新不能通过一条边到达的顶点的最短路径长度,长度还是保持正无穷。
所以,可以将leetcode-743使用FB算法。
1 | class Solution { |
注意上面的flag操作,可以剪枝不必要的循环。
有 n 个城市通过 m 个航班连接。每个航班都从城市 u 开始,以价格 w 抵达 v。
现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是找到从 src 到 dst 最多经过 k 站中转的最便宜的价格。 如果没有这样的路线,则输出 -1。
解法一:
1 | class Solution { |
解法二:
1 | class Solution { |
SPFA
FB对边的松弛操作是盲目的,每次循环都将所有的边拿出来看一下。其实,只有当前节点更新了,以他为起点的终点节点才会被更新,不然是无效的。
SPFA 是 Bellman−Ford 的队列优化,但是算法时间效率不稳定,时间复杂度为 O(E),最好情况下,每个节点只入队一次,就是 BFS,最坏情况下,每一个节点都要入队 V−1 次,这时候就退化成 Bellman−Ford了。SPFA 时间复杂度某种情况下略高于 Dijkstra, 适合稀疏图。
SPFA 是可以用于带有负权图的,在 SPFA 中每一个点松弛过后说明这个点距离更近了,所以有可能通过这个点会再次优化其他点,所以它的策略是将 vis 位置为 false,把这个点入队再判断一次!这就和 Dijkstra 的贪心策略不同了。
SPFA 还有个用处是可以判断图是否存在负环,我们只要用一个 cnt[x] 数组来存放经过这个点的次数,上面提到过,最坏情况下每个节点入队 V−1 次,如果cnt[x] 为 V的个数,那就说明存在负环了。
【算法思想】
- 初始时,只有把起点放入队列中。
- 遍历与起点相连的边,如果可以松弛就更新距离dis[],然后判断如果这个点没有在队列中就入队标记。
- 出队队首,取消标记,循环2-3步,直至队为空。
- 所有能更新的点都更新完毕,dis[]数组中的距离就是起点到其他点的最短距离。
1 | class Solution { |
Floyd算法
本质是动态规划,能解决任意两点间的最短路径,时间复杂度O*(V3) 。
Floyd它是可以判断有没有负权边环的,走N−1 步,如果再走一步,更短了,那么就说明有环。另外 Floyd 是不能处理带有负权的最短路的,因为本质是一个动态规划算法,有了负边,最优子结构的性质就不满足了。由此可见,它能够判断是否存在负环,但是不能够处理带有负权的最短路径。
Floyd 有个神奇的特性,这个是其他算法没有的, Floyd第 k 轮算的结果,是每个源点到每个汇点经过前 k 个点的最短路,这一点可以出题。
对于上题,由于是动态规划,所以都是用邻接矩阵,并且它是不用 dis 数组和 vis 数组的
这边注意,初始化邻接矩阵的时候,如果两个顶点没有边,最好初始化为INF,别初始化为-1,上面说过Floyd是不能处理负权边的,只能判断有没有负环!
1 | class Solution { |
参考
- https://www.dazhuanlan.com/2019/12/08/5dec8b7394f9b/
- https://www.bilibili.com/video/BV11b411S79w?from=search&seid=8294149097754810253
- https://www.bilibili.com/video/BV1gb41137u4?from=search&seid=14565420049859812931
- https://www.bilibili.com/video/BV1Yx411a7HX?p=2
- https://blog.csdn.net/qq_24884193/article/details/104357889


