leetcode-118-杨辉三角1

描述

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

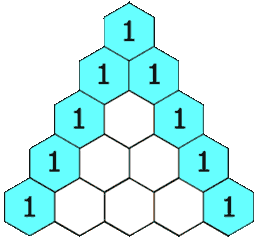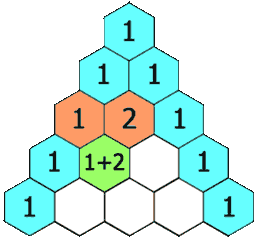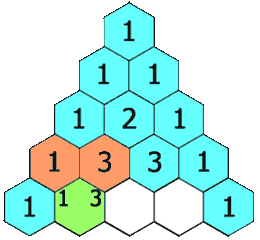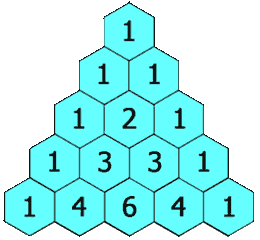
在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]

链接：https://leetcode-cn.com/problems/pascals-triangle

分析

1. 暴力递归：basecase：可以看到，每行的最左边和最右边的数字是1。因此，我们可以将基本情况定义如下: f(i, j)=1 where j=1 or j==i

   递推关系：

   ​ 首先，我们定义一个函数 f(i,j)它将会返回帕斯卡三角形第 i 行、第 j 列的数字。

   我们可以用下面的公式来表示这一递推关系：f(i,j)=f(i−1,j−1)+f(i−1,j)

2. 动态规划：因为暴力递归还有很多值会重复计算，所以使用一个数组保存已经计算过的值。

代码

源码： https://github.com/Castile/algorithm/blob/master/leetcode/src/RecurrenceAndDynamicProgramming/leetcode118_PascalTriangle.java

// 暴力递归： 但是会超时
   public List<List<Integer>> generate(int numRows) {
       List<List<Integer>> triangle = new ArrayList<>();
       if(numRows == 0) return triangle;
       for(int i = 1 ; i <= numRows; i++){
           List<Integer> list =  new ArrayList<>();
           for(int j = 1; j <= i ; j++){
               list.add(calc(i, j));
           }
           triangle.add(list);
       }
       return triangle;
   }
   public int calc(int i, int j){
       if( j == 1 || i == j)   return 1;
       return calc(i - 1, j - 1) + calc(i - 1, j);
   }

动态规划：

// 动态规划
    class Solution {
        public List<List<Integer>> generate(int numRows) {
            List<List<Integer>> triangle = new ArrayList<>();
            int[][] dp = new int[numRows+1][numRows+1];
            if(numRows == 0) return triangle;
            for(int i = 1 ; i <= numRows; i++){
                List<Integer> list =  new ArrayList<>();
                for(int j = 1; j <= i ; j++){
                    list.add(calc(dp, i, j));
                }
                triangle.add(list);
            }
            return triangle;
        }
        public int calc(int[][] dp, int i, int j){
            if( j == 1 || i == j){
                dp[i][j] = 1;
                return 1;
            }
            if(dp[i][j] != 0)   return dp[i][j];
            dp[i][j] = calc(dp, i - 1, j - 1) + calc(dp, i - 1, j);
            return dp[i][j];
        }
    }

相似题目： leetcode-119-杨辉三角2