描述
Leetcode-130: 被围绕的区域
给定一个二维的矩阵,包含 ‘X’ 和 ‘O’(字母 O)。
找到所有被 ‘X’ 围绕的区域,并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。
示例:
X X X X
X O O X
X X O X
X O X X
运行你的函数后,矩阵变为:X X X X
X X X X
X X X X
X O X X
解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 ‘O’ 都不会被填充为 ‘X’。 任何不在边界上,或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
分析
dfs搜索:将边界上的‘O’及其连通的先设置成‘#’标识,这些是不会被填充的,等搜索完毕之后再将这些标志换回‘O’。而在里面的‘O’就是被包围的区域,通过双层循环将里面的’O‘替换成’X‘即可。
并查集:并查集的思想就是,同一个连通区域内的所有点的根节点是同一个。将每个点映射成一个数字。先假设每个点的根节点就是他们自己,然后我们以此输入连通的点对,然后将其中一个点的根节点赋成另一个节点的根节点,这样这两个点所在连通区域又相互连通了。
并查集代码:UF
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60/**
* @author Hongliang Zhu
* @create 2020-01-25 21:25
*/
// 并查集 UF
public class UF {
private int count = 0; // 连通分量
private int[] parent;
// 新增一个数组记录树的“重量”
private int[] size;
// 构造
public UF(int n){ // n个元素
this.count = n;
size = new int[n];
parent = new int[n];
// 一开始每一个节点自成一个集合,都不连通
for (int i = 0; i < n; i++){
parent[i] = i; // 自己的父节点指向自己
size[i] = 1; // 每隔几何只有自身一个元素
}
}
public int find(int x){
int root = parent[x];
while (parent[x] != x){ // 路径压缩
x = parent[x];
}
return x;
}
public boolean isSameSet(int a, int b){
return find(a) == find(b);
}
public int count(){
return count;
}
public void union(int a, int b){
int rootA = find(a);
int rootB = find(b);
if(rootA == rootB){
return; // 同一个集合不能合并
}else{
if(size[rootA] > size[rootB]){
parent[rootB] = rootA;
size[rootA] += size[rootB];
}else {
parent[rootA] = rootB;
size[rootB] += size[rootA];
}
}
count--; // 连通分量个数减一
}
}可以把那些不需要被替换的
O看成一个拥有独门绝技的门派,它们有一个共同祖师爷叫 **dummy**,这些O和dummy互相连通,而那些需要被替换的O与dummy不连通。 如下图: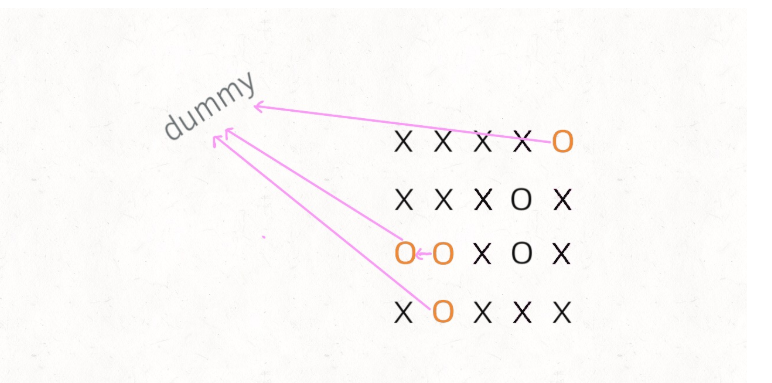
首先要解决的是,根据我们的实现,Union-Find 底层用的是一维数组,构造函数需要传入这个数组的大小,而题目给的是一个二维棋盘。
这个很简单,二维坐标
(x,y)可以转换成x * n + y这个数(m是棋盘的行数,n是棋盘的列数)。敲黑板,这是将二维坐标映射到一维的常用技巧。 其次,我们之前描述的「祖师爷」是虚构的,需要给他老人家留个位置。索引
[0.. m*n-1]都是棋盘内坐标的一维映射,那就让这个虚拟的dummy节点占据索引m * n好了。 我们的思路是把所有边界上的 O看做一个连通区域。遇到 O 就执行并查集合并操作,这样所有的 O 就会被分成两类
- 和边界上的 O在一个连通区域内的。这些 O 我们保留。
- 不和边界上的O 在一个连通区域内的。这些 O 就是被包围的,替换。
代码
dfs版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42class Solution {
int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public void solve(char[][] board) {
if(board == null || board.length == 0)
return;
int m = board.length;
int n = board[0].length;
// 边缘搜索
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if((i == 0 || j == 0 || i == m-1 || j == n-1) && (board[i][j] == 'O')){
dfs(board, i, j);
}
}
}
//
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(board[i][j] == 'O'){
board[i][j] = 'X';
}
if(board[i][j] == '#'){
board[i][j] = 'O';
}
}
}
}
public void dfs(char[][] board, int i, int j){
if(i < 0 || j < 0 || i >= board.length || j >= board[0].length || board[i][j] != 'O')
return;
board[i][j] = '#';
for(int[] d: directions){
dfs(board, i+d[0], d[1]+j);
}
}
}
并查集
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41// 使用并查集解决
public static void solveUF(char[][] board) {
if(board==null || board.length == 0)
return;
int m = board.length;
int n = board[0].length;
// 边界上的‘O’的根节点都是dummy
UF uf = new UF(n * m + 1);// 增加一个存储dummy节点
int dummy = m * n;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(board[i][j] == 'O'){ // 目标
if(i == 0 || j == 0 || i == m -1 || j == n -1) { // 如果是边界上的'O', 与dummy合并
uf.union(i*n+j, dummy);
}else{ // 里面的
// 方向数组 d 是上下左右搜索的常用手法
int[][] d = new int[][]{{1,0}, {0,1}, {0,-1}, {-1,0}};
// 将此 O 与上下左右的 O 连通
for (int k = 0; k < 4; k++) {
int x = i + d[k][0];
int y = j + d[k][1];
if (board[x][y] == 'O')
uf.union(x * n + y, i * n + j);
}
}
}
}
}
for (int i = 1; i < m-1; i++){
for( int j = 1; j < n-1; j++){
if(!uf.isSameSet(i*n+j, dummy)){
board[i][j] = 'X';
}
}
}
}
参考:


